|
Karnaugh Maps We know that a boolean expression can be simplified algebraically.The drawback of that method is that if you are confronted with a little complex expression, it becomes very difficult and very time consuming to simplify it.This problem is overcome by Karnaugh maps(or K maps).This is a straight forward method to simplify a boolean expression.
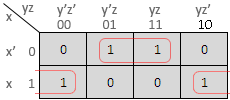
Two Variable Karnaugh maps :
Three Variable Karnaugh maps : A three variable K-map can be drawn as follows :
One important thing to remember while constructing a three variable K-map is the order in which we place the minterms / maxterms.Note that in the first row we have m3 after m1 followed by m2.Similarly m7 is present after m5 followed by m6.This order must be maintained for all three or more variable K-maps.
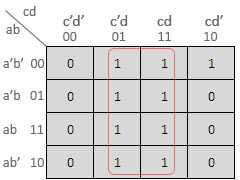
Four Variable Karnaugh maps : A four variable K-map is shown below.
Simplification Procedure for Karnaugh maps Pair Reduction Rule : Remove the variable which changes its state from complemented to uncomplemented or vice versa.Pair removes one variable only.
Quad Reduction Rule : Remove the two variables which change their states.A quad removes two variables.
Octet Reduction Rule : Remove the three variables which changes their state.Octet removes three variables.
Map Rolling : Map rolling means roll the map considering the map as if its left edges are touching the right edges and top edges are touching bottom edges.While marking the pairs quads and octet, map must be rolled.
Overlapping Groups : Overlapping means same 1 can be encircled more than once. Overlapping always leads to simpler expressions.
Redundant Group : It is a group whose all 1's are overlapped by other groups. Redundant groups must be removed. Removal of redundant group leads to much simpler expression.
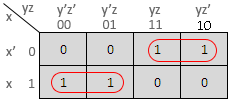
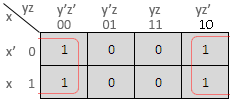
Ex. 1 : Represent the following boolean expression in a K-map and simplify. F = x'yz + x'yz' + xy'z' + xy'z Solution : The K-map is as follows :
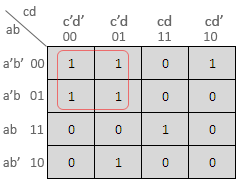
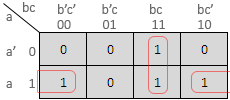
Hence the simplified expression is F = x'y + xy' Ex. 2 :Simplify the following boolean expression using K-map. F = a'bc + ab'c' + abc + abc' Solution : The K-map is as follows :
Hence the simplified expression is F = bc + ac' |
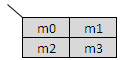 This is how you will place the minterms / maxterms for a two variable K- map.
This is how you will place the minterms / maxterms for a two variable K- map.